[백준] 2133번 타일 채우기 - C/C++
https://www.acmicpc.net/problem/2133
2133번: 타일 채우기
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
www.acmicpc.net
문제
3 ×N 크기의 벽을 2 ×1, 1 × 2 크기의 타일로 채우는 경우의 수를 구해보자.
입력
첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.
출력
첫째 줄에 경우의 수를 출력한다.
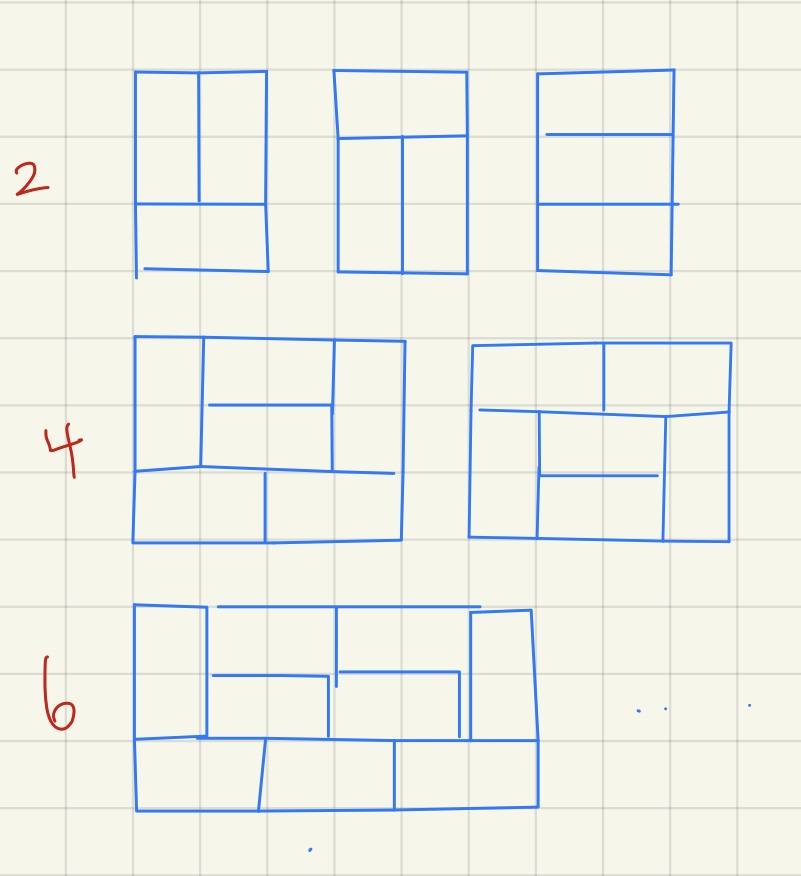
문제에서 주어진 힌트와 같이 2개 단위로 커질 때마다 그 타일을 이 전 타일들로 만들지 못하는 유일한 타일 배치가 2개씩 생기게 된다. 2개만 유일하게 3가지의 경우가 가능하다.
입력값으로 홀수가 주어지게 된다면 3*N 이 총홀수개의 단일 타일이 필요하게 되므로 만들 수 있는 경우의 수는 없다.
짝수가 들어올 경우 본인만의 유일한 타일 갯수 2개 , 3가지의 3*2 타일을 배치하고 (본인-2)를 배치하거나 3*4의 타일 2개를 배치하고 (본인-4)를 배치하거나... 가 된다. 이렇게 이 전 타일들을 먼저 구해 놓으면 타일을 만들 경우의 수를 모두 구할 수 있다.
#include <iostream>
#include <cstring>
using namespace std;
int N, sum = 0;;
int dp[31] = { 0 };
int main() {
cin >> N;
memset(dp, 0, sizeof(dp));
dp[2] = 3;
for (int i = 4; i <= 30; i += 2) {
dp[i] += 2;
dp[i] += 3 * dp[i - 2];
for(int idx = 4 ; idx <= i;idx+=2 )
dp[i] += 2 * dp[i - idx] ;
}
cout << dp[N] << "\n";
return 0;
}처음에는 문제의 힌트를 안보고 3가지 경우의 수만 있는 줄 알고 제출했으나 틀렸다. 그렇게 4를 만들 수 있는 타일을 보고 4까지만 특별한 경우가 있는 줄 알고 재귀 형식의 코드와 반복문 형식의 코드를 모두 짰으나 틀렸다. 다시 곰곰이 생각해보다 2가 증가할 때마다 유일한 타일 배치가 생겨나는 것을 알고 코드를 짜서 맞게 되었다.
원래 이런 단순 점화식 문제는 잘 풀지 않는데 친구가 풀자고 하여 이번 기회에 접하게 되었다. 이런 단순 점화식 문제는 코드를 짜는 것보다 점화식만 구하면 코딩은 쉽다는 생각에 잘 풀지 않았는데 생각해낸 규칙을 점화식으로 만들고 그것을 또 코드로 옮기는 것이 아무 실수가 없진 않았다. 이러한 문제도 종종 연습해야겠다!