https://www.acmicpc.net/problem/14890
14890번: 경사로
첫째 줄에 N (2 ≤ N ≤ 100)과 L (1 ≤ L ≤ N)이 주어진다. 둘째 줄부터 N개의 줄에 지도가 주어진다. 각 칸의 높이는 10보다 작거나 같은 자연수이다.
www.acmicpc.net
문제
크기가 N×N인 지도가 있다. 지도의 각 칸에는 그 곳의 높이가 적혀져 있다.
오늘은 이 지도에서 지나갈 수 있는 길이 몇 개 있는지 알아보려고 한다. 길이란 한 행 또는 한 열 전부를 나타내며, 한쪽 끝에서 다른쪽 끝까지 지나가는 것이다.
다음과 같은 N=6인 경우 지도를 살펴보자.
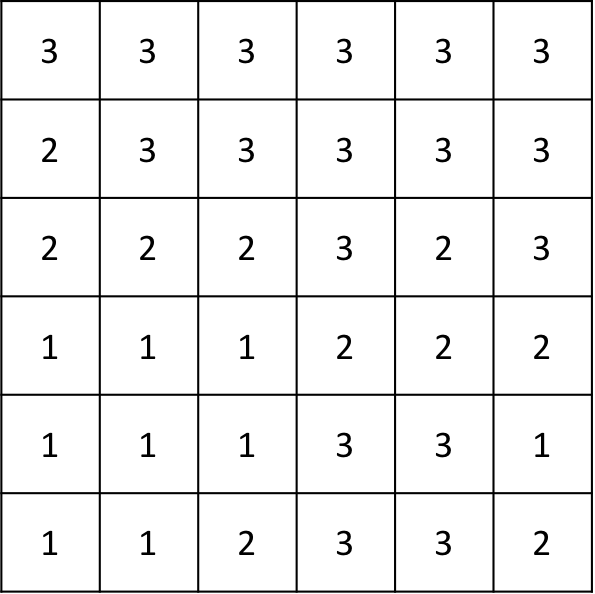
이때, 길은 총 2N개가 있으며, 아래와 같다.
길을 지나갈 수 있으려면 길에 속한 모든 칸의 높이가 모두 같아야 한다. 또는, 경사로를 놓아서 지나갈 수 있는 길을 만들 수 있다. 경사로는 높이가 항상 1이며, 길이는 L이다. 또, 개수는 매우 많아 부족할 일이 없다. 경사로는 낮은 칸과 높은 칸을 연결하며, 아래와 같은 조건을 만족해야한다.
- 경사로는 낮은 칸에 놓으며, L개의 연속된 칸에 경사로의 바닥이 모두 접해야 한다.
- 낮은 칸과 높은 칸의 높이 차이는 1이어야 한다.
- 경사로를 놓을 낮은 칸의 높이는 모두 같아야 하고, L개의 칸이 연속되어 있어야 한다.
아래와 같은 경우에는 경사로를 놓을 수 없다.
- 경사로를 놓은 곳에 또 경사로를 놓는 경우
- 낮은 칸과 높은 칸의 높이 차이가 1이 아닌 경우
- 낮은 지점의 칸의 높이가 모두 같지 않거나, L개가 연속되지 않은 경우
- 경사로를 놓다가 범위를 벗어나는 경우
L = 2인 경우에 경사로를 놓을 수 있는 경우를 그림으로 나타내면 아래와 같다.

경사로를 놓을 수 없는 경우는 아래와 같다.

위의 그림의 가장 왼쪽부터 1번, 2번, 3번, 4번 예제라고 했을 때, 1번은 높이 차이가 1이 아니라서, 2번은 경사로를 바닥과 접하게 놓지 않아서, 3번은 겹쳐서 놓아서, 4번은 기울이게 놓아서 불가능한 경우이다.
가장 위에 주어진 그림 예의 경우에 지나갈 수 있는 길은 파란색으로, 지나갈 수 없는 길은 빨간색으로 표시되어 있으며, 아래와 같다. 경사로의 길이 L = 2이다.

지도가 주어졌을 때, 지나갈 수 있는 길의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N (2 ≤ N ≤ 100)과 L (1 ≤ L ≤ N)이 주어진다. 둘째 줄부터 N개의 줄에 지도가 주어진다. 각 칸의 높이는 10보다 작거나 같은 자연수이다.
출력
첫째 줄에 지나갈 수 있는 길의 개수를 출력한다.
구현 문제이다. 구현 문제는 흐름에 따라 분기처리를 잘해주어야 한다!
가장 중요한 포인트는 경사로를 설치하는 기준이다. 경사로는 오르막과 내리막이 있는 데 이 두 개가 설치하는 조건이 다르다.
- 현재 위치에서 나와 같은 칸을 만났을 경우
일단 1칸 전진한다. 이는 그냥 전진한 것일 수도 있고 오르막을 오르는 중일 수도 있다.
- 현재 위치에서 나보다 1칸 높은 칸을 만났을 경우
현재 위치에서부터 같은 높이의 칸의 개수가 L 보다 크거나 같으면 [현재위치 - (L - 1)] ~ [현재 위치] 만큼 오르막을
설치할 수 있다. 이 경우가 앞서 말한 오르막을 오르는 중이었던 것이다.
- 현재 위치에서 나보다 1칸 낮은 칸을 만났을 경우
다음 칸부터 L 칸의 거리가 모두 같은 경우 내리막을 설치할 수 있다.
이때 앞으로의 L 칸은 평평하지 않기 때문에 현재까지 같은 높이를 경사로가 끝까지 놓인 다음 칸에서 1이 될 수 있도록
1 - L로 설정한다.
- 그 외의 경우
진행할 방법이 없으므로 길이 아니다.
#include <iostream>
#include <algorithm>
using namespace std;
int N, L,a;
int mat[101][101] = {0};
int arr[101];
int ans = 0,idx,cnt;
bool validUp(){
if(cnt >= L)
return true;
return false;
}
bool validDown(){
for(int i = 1 ; i <= L ;i++){
if(arr[idx] - 1 != arr[idx + i])
return false;
}
return true;
}
bool checkRoad(){
idx = 0;
cnt = 1;
while(1){
if(idx == N - 1)
return true;
if(arr[idx] == arr[idx + 1]){
idx++;
cnt++;
}
else if (arr[idx] + 1== arr[idx + 1]){
if(validUp()){
idx++;
cnt = 1;
}
else
return false;
}
else if (arr[idx] - 1 == arr[idx + 1]){
if(validDown()){
idx++;
cnt = 1 - L;
}
else return false;
}
else
return false;
}
}
int main (){
cin >> N >> L;
for(int i = 0 ; i < N ;i++){
for(int j = 0 ; j < N ;j++){
cin >> a;
mat[i][j] = a;
}
}
for(int i = 0 ; i < N ; i++){
for(int j = 0 ; j < N ;j++){
arr[j] = mat[i][j];
}
if(checkRoad()) ans++;
for(int j = 0 ; j < N ;j++){
arr[j] = mat[j][i];
}
if(checkRoad()) ans++;
}
cout << ans;
}그동안 안 푼 문제를 풀고 있는 중이다. 골드 3 난이도에서 눈에 보이는 것 중 이 문제만 풀지 않았길래 들어가 봤더니 구현문제였다! 아무래도 구현문제는 오래 걸린다는 생각에 잘 풀지 않았던 것 같다. 현재 위치에서 앞으로의 길에 오르막 또는 내리막을 설치할 생각만 하였더니 분기 처리를 하기가 너무 어려웠다. 내리막의 경우 내 다음칸부터 설치, 오르막의 경우 내 위치부터 설치하는 것으로 생각하였더니 처리가 너무 어려웠다. 그래서 힌트를 보니 오르막은 앞서 온 길을 생각하는 것이 포인트였다! 좋은 문제인 것 같다.
'코딩 > 백준' 카테고리의 다른 글
| [백준]2146번 다리 만들기 - C++ (0) | 2023.01.16 |
|---|---|
| [백준]1717번 집합의표현 - C++ (0) | 2023.01.13 |
| [백준]3190번 뱀 - C++ (0) | 2023.01.11 |
| [백준]2589번 보물섬 - C++ (0) | 2023.01.06 |
| [백준]3055번 탈출 - C++ (0) | 2023.01.04 |